Complete an adaptive assignment

Jump to section

Interpret the adaptive assignment Grade Report page

An adaptive assignment is created by designing different question branches, with each branch usually representing a difficulty level (Example — easy, medium, and difficult).

NOTE: Your instructor might instead design the branches to be categorized as concepts or topics instead of difficulty level.

NOTE: The number of branches and questions for an adaptive assignment can vary.

Each question is presented to you one at a time and your performance on earlier questions determines which question branch the next question is retrieved from.

IMPORTANT: Partial grading isn't permitted on adaptive assignments.

This navigation between branches can vary and is configured by your instructor (Example — your instructor could configure the adaptive assignment such that submitting two consecutive correct answers on the easy branch will navigate you to the medium branch).

During your attempt, an adaptive assignment looks quite similar to most non-adaptive assignments, and you'll interact with it in much the same way as you would most non-adaptive assignments.

NOTE: Adaptive assignments are configured to not allow answers to be resubmitted (you can't go back to previous questions during your attempt). This is indicated on the assignment's launch page.

The launch page is shown with "No" in the "Resubmit Responses" field of the Properties section.

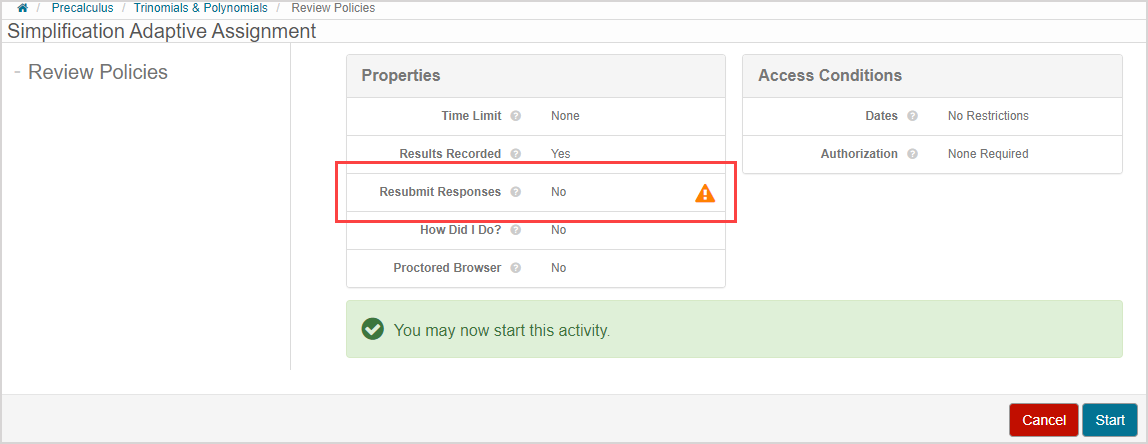
Check out Review the launch page for reminders of other important information that can be displayed on an activity’s launch page.

Your instructor might configure the adaptive assignment to display a progress graph which is visible during your attempt and on the Grade Report page.

The Grade Report page displays your branch performance summary and overall score, and is displayed once you've submitted your attempt.

NOTE: An adaptive assignment is just one of the assignment types that your instructor can create. Check out Learn about the different activity types to see what other types of assignments you might come across.

TIP: Adaptive assignments are different from adaptive questions. Check out Complete an adaptive question to learn more about these differences.

Interpret the progress graph

NOTE: Your adaptive assignment might be configured to not display the progress graph.

Your instructor can configure the adaptive assignment to display a progress graph that's visible (A) during your attempt and (B) on the Grade Report page.

The progress graph is shown above a question during an attempt, and below the grade report data on the grade report page.

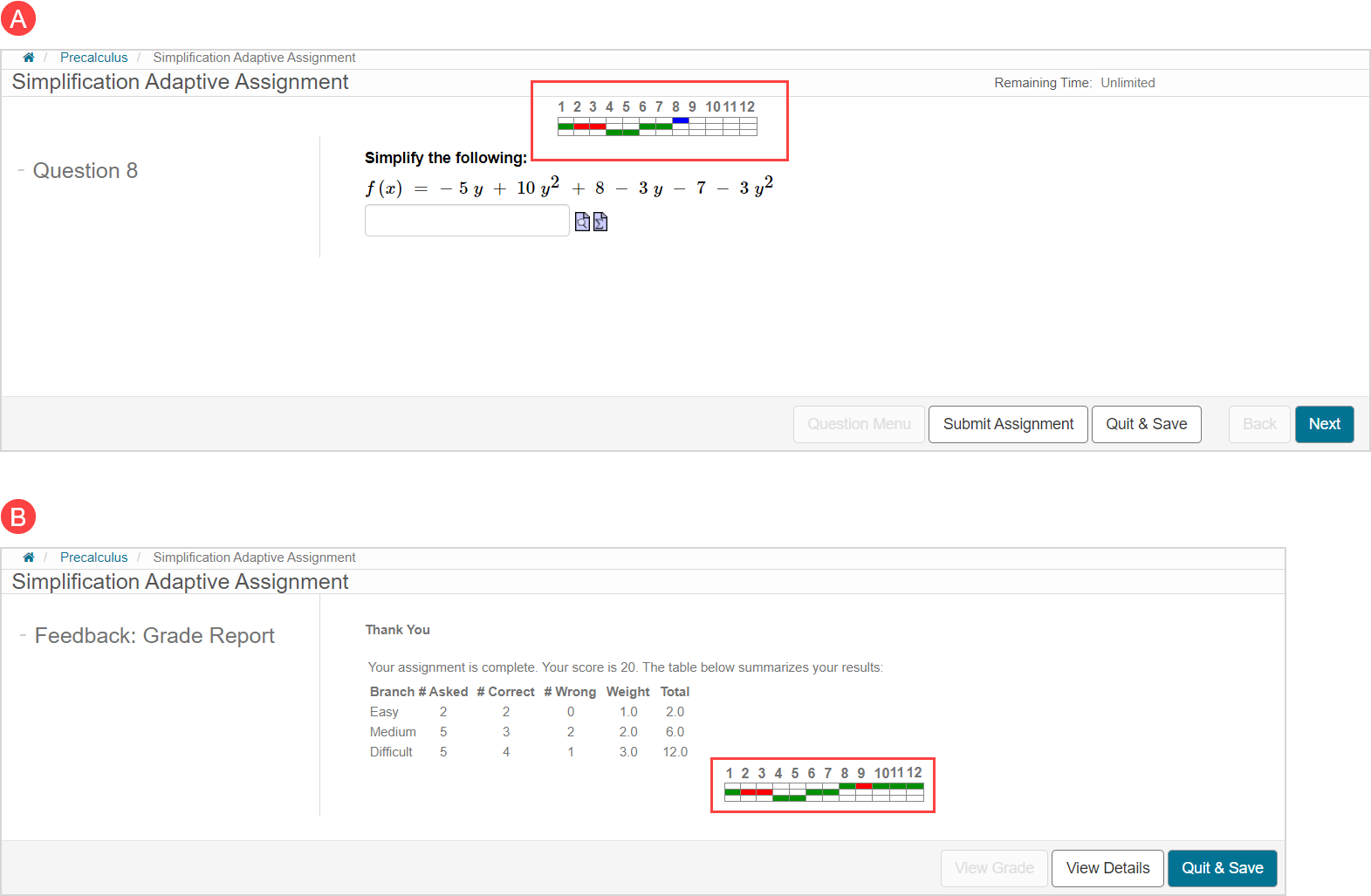
This progress graph indicates where you are in the adaptive question branching system and tracks the correctness of your responses to the questions:

A sample progress graph showing 12 questions across 3 difficulty levels with all three colour indicators in different cells that indicate correctness and status: red, blue, and green.

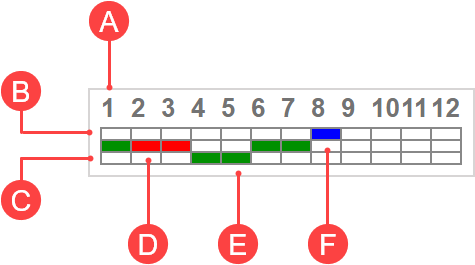
A. The question list within the adaptive assignment.

B. The branch with the highest difficulty level.

C. The branch with the lowest difficulty level.

D. A red cell indicates an incorrect response.

E. A green cell indicates a correct response.

F. A blue cell indicates the current question being attempted.

NOTE: The (B) highest difficulty branch and (C) lowest difficulty branch represent the branching structure of most adaptive assignments which is based on difficulty level (Example — easy, medium, and difficult). It's possible for the branching of your adaptive assignment to contain more or less than three branches, and be based on different topics or concepts instead of difficulty level. Contact your instructor if you have questions about the branching design for your adaptive assignment.

Interpret the adaptive assignment Grade Report page

Your performance on the adaptive assignment is represented on the adaptive assignment Grade Report page once you've submitted your attempt.

This page displays your:

The Grade Report page shows your score, score breakdown in table form, and a progress graph (if enabled).

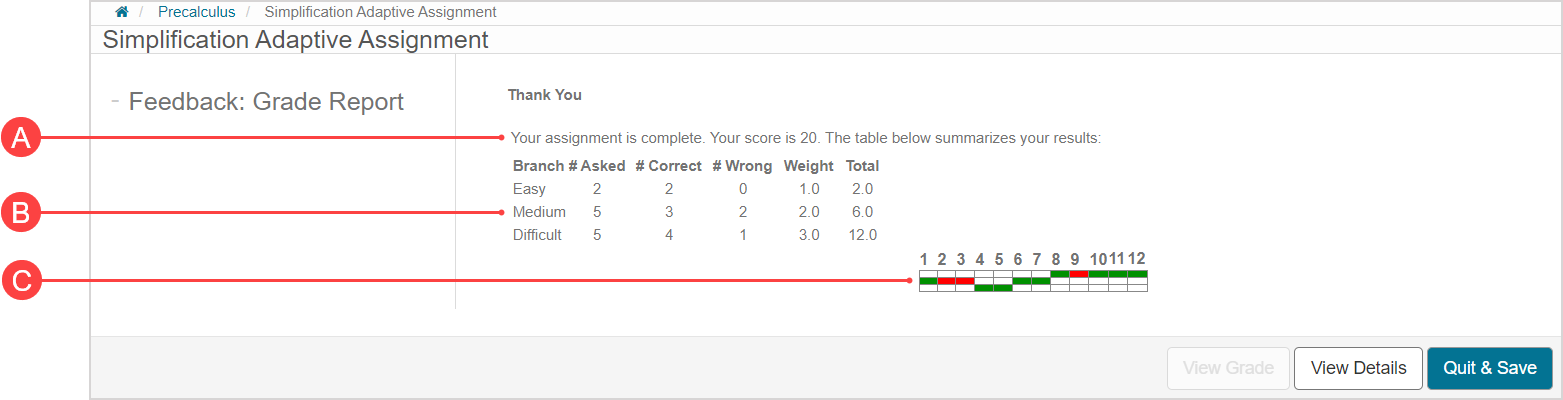
A. Overall score

B. Branch performance summary

C. Progress graph (if enabled)

NOTE: By default, your (A) overall score on the adaptive assignment is represented by the sum of the branch scores in the Total column of the adaptive assignment Grade Report.

The last column of the grade summary table is the "Total" column.

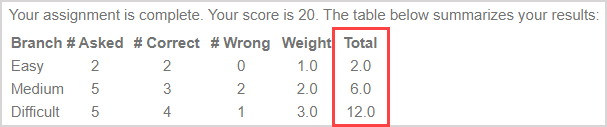
Does your overall score not match the sum of the branch scores? That's because your instructor chose to use a different grade policy. Contact your instructor for clarification on this overall score calculation.