View example Maple grading code

Maple-graded questions pass the student's response to the Maple^TM math engine.

Maple runs the grading code that's defined in the Grading Code field of the question to generate the student's grade.

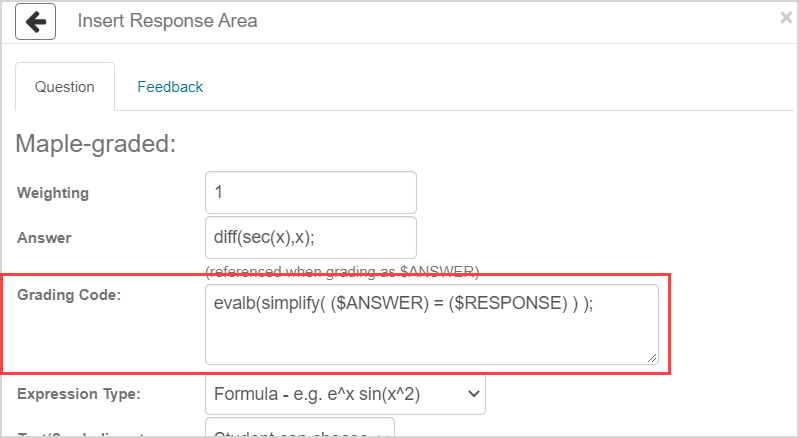
You can use customize the grading code for Maple-graded questions to take advantage of the robust capabilities of the Maple engine to:

• Test equivalence of different mathematical objects
• Develop partial grading
• Allow for tolerances in your correct answer
• And much more...

View these grading code examples (entered in the Grading Code field) to help get you started with your question authoring:

Typical numerical and expression responses

These examples of grading code assume that the correct answer is already defined in the Answer field:

Default grading code

1
evalb(($ANSWER)-($RESPONSE)=0);

Simplify student response

1
is(($ANSWER)-($RESPONSE)=0);

Absolute margin of error of numeric answers

• This example has an absolute margin of error of 0.01.

1
is(abs(($ANSWER)-($RESPONSE))<=0.01);

Symbolic expressions

1
evalb(simplify(($ANSWER)-($RESPONSE),symbolic)=0);

Other mathematical objects as student responses

These examples of grading code apply to the Maple syntax sub-type (the Expression Type is set to Maple Syntax):

Equations

• Assumes that the Answer field contains an equation.

1
2
3
4
5
6
7
8
9
EquivEQ := proc( A :: {equation,algebraic}, B :: {equation,algebraic}, { params :: set := {} } )
  local phi, X, Y, k, sol:
  phi := u -> piecewise( type( u, equation ), lhs(u) - rhs(u), u ):
  X := simplify( phi(A) ): 
  Y := simplify( phi(B) ):
  sol := solve( { X = k * Y, k <> 0 }, k ):
  is( numelems( sol ) = 1 and indets( sol ) = { k } union params ):
end proc:
EquivEQ( $RESPONSE, $ANSWER );

Matrices

• Assumes that the Answer field contains the Matrix command from Maple.

TIP: Check out Matrix command from the Maple online help site for notes on the Matrix command.

1
LinearAlgebra:-Equal($RESPONSE,$ANSWER);

Matrices with display

• Assumes that your question algorithm contains the answer as a Matrix command from Maple in the variable $a.

TIP: Check out Matrix command from the Maple online help site for notes on the Matrix command.

• Enter this code in the Answer field:

1
printf(MathML:-ExportPresentation($a));

• Enter this code in the Grading Code field:

1
LinearAlgebra:-Equal($RESPONSE,$a);

Sets

• Assumes the student response and correct answer are given with set braces (Example — {a,b}).

1
comparray($RESPONSE,$ANSWER,dontprint);

Sets with partial grading

• Permits partial grading for each correct element.

1
2
3
if numelems($RESPONSE)>numelems($ANSWER) then 0.0
else evalf(numelems($RESPONSE intersect $ANSWER)/numelems($ANSWER))
end if;

Factored polynomials

• Students must enter a fully factorized polynomial (in x) that's mathematically equivalent to the defined correct answer.

1
2
is(product({op(RESPONSE)}[i],i=1..nops({op(RESPONSE)}))-ANSWER=0) and
andmap(u -> `or`(is(irreduc(u) and gcd(coeffs(u)) = 1), is(degree(u) = 0), is(subs(x = 0, u) = 0 and numelems([coeffs(u, x)]) = 1)), {op(RESPONSE)});

General solutions to equations

Differential equation

• Checks that the response is a solution of L.

TIP: Make sure to edit the right-hand side of the definition of L to match your differential equation.

1
2
3
R:=$RESPONSE;
L:=y->diff(y,t,t)+y; # edit for your differential operator
is(L(R)=0) and evalb(numelems(indets(R,name))=numelems(indets($ANSWER,name)));  

Integrals

• With respect to x.
• Students can use any constant of integration.
• Assumes that the Answer field contains the general solution.

1
is(diff(($ANSWER)-($RESPONSE),x)=0);

Constant multiples of an expression

• Checks if the student's response is a constant multiple of the expression that's defined in the Answer field.

1
2
sol:=solve({$RESPONSE = k*$ANSWER, k <> 0},k);
is(numelems(sol) = 1 and indets(sol) = {k});

Require student responses in a specific form

Simplified polynomials

• Students must enter the polynomial (in terms of x) in fully simplified form as it's defined in the Answer field.

1
2
R:="$RESPONSE";
is(($ANSWER)-(parse(R))=0 and StringTools:-CountCharacterOccurrences(R,"x") = degree(ANSWER));

Prevent cheating via entry of Maple code

• In this example, if the answer is calculated by factor(x^2-1) in Maple code, then this example will detect if the Maple command factor is used by the student, and grade incorrect. Only required for a Maple Syntax sub-type question.

1
evalb(StringTools[Search]("factor","$RESPONSE")=0) and evalb($RESPONSE=factor(x^2-1));

Same form

• Requires the student response to be in the exact same form that the correct answer is within the Answer field.

1
2
3
ia:=InertForm[Parse]("$ANSWER");
ir:=InertForm[Parse]("$RESPONSE");
is(value(ia)=value(ir) and op(0,ia)=op(0,ir) and map(value,{op(ia)})=map(value,{op(ir)}));

Define the margin of error for numeric responses

These examples of grading code reproduce the margin of error logic from a numeric question within a Maple-graded question:

TIP: Check out Author a numeric question.

Absolute accuracy

• Requires the student to answer with absolute accuracy compared to the correct answer defined in the Answer field without the use of arithmetic.

1
InertForm:-SameStructure(InertForm:-Parse("$RESPONSE"), $ANSWER);

Absolute accuracy with significant figures

• Requires the student to answer with absolute accuracy and the same number of significant figures as the correct answer within the Answer field.

1
evalb(($ANSWER)-($RESPONSE)=0 and StringTools:-Length("$ANSWER")=StringTools:-Length("$RESPONSE"));

No arithmetic

• Arithmetic isn't accepted and this requirement can be combined with other statements.

1
evalb(StringTools:-CountCharacterOccurrences(convert(InertForm:-Parse("$RESPONSE"), 'string'),"%")=0);

Absolute margin of error

• This example has an absolute margin of error of 0.1.

1
evalb(abs(($ANSWER) - ($RESPONSE)) <= 0.1);

Percentage margin of error

• This example has a percentage margin of error of 1%.

1
evalb(100*abs((($ANSWER) - ($RESPONSE))/($ANSWER)) <= 1);