View available functions for algorithmic questions
Jump to section:
eq(a, b), ge(a, b), le(a, b), ne(a, b)
max(a, b, c, d, ...), min(a, b, c, d, ...)
plotmaple("plotstatement,...")
Random integer generation: range(n), range(m, n), range(m, n, k)
Random integer generation: rint(n), rint(m, n), rint(m, n, k)
Rounding: int(x), maple("MapleTA:-Builtin:-decimal(n, x)"), maple("MapleTA:-Builtin:-sig(n, x)")
Standard mathematical functions: sin(x), cos(x), tan(x), ...
Use the following built-in functions when authoring algorithmic questions:
TIP: Check out Follow Algorithm Editor syntax rules to learn about manually entering correct command line syntax in the Algorithm Editor.
TIP: Check out Optimize your algorithm for some best practices when authoring your algorithm.
NOTE: The following functions are intended for question authoring and can't be used by students for their responses (with the exception of the standard mathematical functions).
NOTE: When a number is entered in the Algorithm Editor, the default behavior is that the comma is added as the thousands separator and trailing zeros are truncated and not displayed. Example —Entering 2909.0000 in the Algorithm Editor returns 2,909.
condition:x
Imposes the condition defined by statement x, which is typically constructed using 1 or more other functions.
Example —
$a=range(-10,10);
condition: ne($a,0);
Generates a random non-zero integer between -10 and 10 (inclusive).
eq(a, b), ge(a, b), le(a, b), ne(a, b)
eq(a, b) — Returns 1.0 if a and b are equal. Otherwise, it returns 0.0.
Example —
if(eq($a, $b), "Red", "Green");
- Returns Red if $a=$b, and Green otherwise.
ge(a,b) — Returns 1.0 if a is greater than or equal to b. Otherwise, it returns 0.0.
Example —
if(ge($a, $b), "Red", "Green");
- Returns Red if $a>=$b, and Green otherwise.
le(a,b) — Returns 1.0 if a is less than or equal to b. Otherwise, it returns 0.0.
Example —
if(le($a, $b), "Red", "Green");
- Returns Red if $a<=$b, and Green otherwise.
ne(a,b) — Returns 1.0 if a and b are not equal. Otherwise, it returns 0.0.
Example —
if(ne($a, $b), "Red", "Green");
- Returns Red if $a and $b are not equal, and Green otherwise.
fact(n)
Returns factorial n.
If n is not an integer, fact(int(n)) is returned.
If n is negative, 1 is returned.
Example —
fact(4);
- Returns 24
frac(a, b)
Returns a string that expresses the fraction a/b in its lowest terms.
Example —
frac(12, 15);
- Returns 4/5
Example —
frac(12, 3);
- Returns 4
TIP: frac(a,b) can be combined with mathml(s) to produce nicely typeset fractions.
Example —
mathml(frac(8, 12));
- Returns
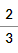
gcd(a, b)
Returns the greatest common divisor of a and b.
Example —
gcd(12, 15);
- Returns 3
gt(a, b), lt(a, b)
gt(a, b) — Returns 1.0 if a is greater than b (a > b). Otherwise, it returns 0.0.
Example —
gt(5, 2);
- Returns 1
Example —
gt(2, 5);
- Returns 0
Example —
gt(5, 5);
- Returns 0
lt(a, b) — Returns 1.0 if a is less than b (a < b). Otherwise, it returns 0.0.
Example —
lt(2, 5);
- Returns 1
Example —
lt(5, 2);
- Returns 0
Example —
lt(5, 5);
- Returns 0
if(a, b, c)
If a is nonzero, it returns b.
Otherwise, it returns c.
Example —
if(2, 4, 6);
- Returns 4
Example —
if(0, 4, 6);
- Returns 6
indexof(k, a, b, c, d, ...)
Returns the index of an item within a list based on the position stated by k (the first item is in position 0, the second in position 1, and so on).
Example —
indexof(3, 2, 3, 5, 7, 11);
- Returns 1 (because 3 is in position 1 of the list)
java(cn, a, b, c, d, ...)
Passes the arguments a,b,c,d,.. to a custom Java™ evaluation engine and return the result.
The first argument (cn) must be a string giving the fully qualified name of a Java class that implements the interface: gateway.question.random.AlgorithmicFunction.
This interface has a single public method: public String eval(String[ ] args);
The arguments a,b,c,d,... are passed to eval() in a string array.
Example —
java("com.mycompany.QuoteFunction", "AAPL")
- Returns a real-time quote for Apple Inc. stock (assuming that the class QuoteFunction had been suitably programmed).
lsu(n, x)
The least significant unit of x in the nth place.
Returns the unit in the nth significant place of x.
Example —
lsu(3, 3.14159);
- Returns 0.01 (the unit in the third significant place).
TIP: This operation is designed to be used when setting the tolerance for correct answers.
Example — For answers to be accepted within a tolerance of 1 unit in the third significant digit:
$ans = <formula>;
$tol = lsu(3, $ans);
Then set the answer field to:
$ans ? $tol
maple("...")
Passes the string to the Möbius math engine (MapleNet™) and returns the result of the last line of Maple code that was processed.
Example —
maple("ithprime(12)");
- Returns 37 (the 12th prime number)
Example —
maple("diff(sin(x)*x, x)");
- Returns cos(x)*x + sin(x)(the derivative of sin(x)*x with respect to x)
Example —
maple("MapleTA:-Builtin:-decimal(1, 6.56)");
- Returns 6.6 (rounds the number 6.56 to 1 decimal place).
TIP: Check out Maple syntax from the Maplesoft website for a comprehensive guide to the Maple programming language, and an index of all available Maple functions and the required syntax.
TIP: Multiple lines of Maple code (separated by semi-colons) are supported using the following structure: $a=maple("line1; line2; line3;");.
TIP: You can also obtain multiple results from the maple("...") function by including the switch command. Check out Optimize your algorithm.
mathml(f)
Returns a string consisting of the formula f typeset in MathML.
MathML tags don't appear on the screen when the value of the string is displayed.
Möbius renders the MathML that's displayed.
Example —
mathml("x^n");
- Returns
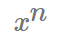
TIP: mathml(f) automatically simplifies the formula by default. Use the "nosimplify" option to prevent auto-simplification.
Example —
mathml("x^2 + 4/8", "nosimplify");
- Returns
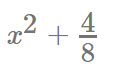
max(a, b, c, d, ...), min(a, b, c, d, ...)
max(a, b, c, d, ...) — Returns the largest of the arguments.
Example —
max(3,5,7,4.8,-1);
- Returns 7
min(a, b, c, d, ...) — Returns the smallest of the arguments.
Example —
max(3,5,7,4.8,-1);
- Returns -1
not(a)
Returns 1.0 if a is equal to 0.0.
Otherwise, it returns 0.0.
Example —
not(6);
- Returns 0
Example —
not(0);
- Returns 1
numfmt(fmt, x)
Returns the value of x, formatted according to the template given by the string fmt.
Example —
numfmt("#,###.00", 2020.9);
- Returns 2,020.90
TIP: The template string fmt has the same specification as the java.text.DecimalFormat command in Java. Check out DecimalFormat in java for help with this function.
plotmaple("plotstatement,...")
Möbius uses MapleNet™ plotting features to graphically display data and mathematical expressions as plots.
IMPORTANT: You can only have 1 set of quotations in your plotmaple function.
Example — $a=plotmaple("plot(sin(x), x = -2*Pi .. 2*Pi, title = "Sine\nGraph", titlefont = ["Roman", 15])"); will give an error.
Example — $a=plotmaple("plot(sin(x), x = -2*Pi .. 2*Pi, title = `Sine\nGraph`, titlefont = [`Roman`, 15])"); will be displayed properly.
TIP: A caption can be added to the plotmaple function to act as both a text caption for the plot as well as alternate text. The caption can include algorithmic variables. Example — plotmaple("plot(sin(x), caption='This is a plot of sin of x')");
plotmaple("plotstatement") — runs the Maple code and outputs the resulting plot as a JPEG or GIF file.
TIP: Check out these other topics to learn what types of Maple plot options you can use in your plot statement.
Example —
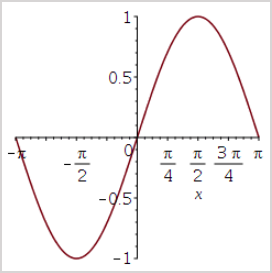
plotmaple("plot(sin(x))");
- Returns:
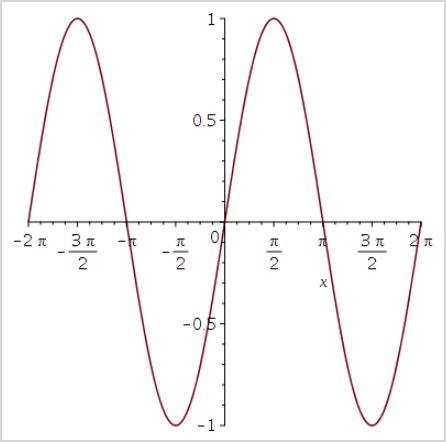
Example —
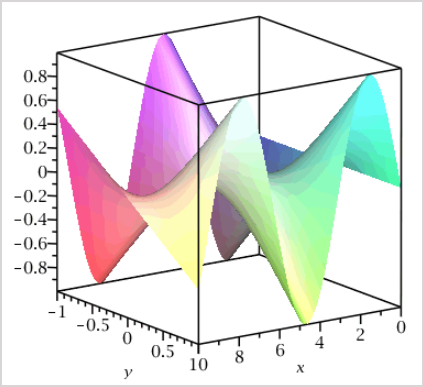
plotmaple("plot3d(sin(x)*y, x=0..10, y=-1..1, style=patchnogrid, lightmodel=light1)");
- Returns:
plotmaple("plotstatement, plotdevice, plotoptions") — runs the Maple code (plotstatement) with gif (to produce a GIF/ANIMATED-GIF) or jpeg (to produces a 24-bit color JPEG) inputs for the plot device argument (plotdevice). Display options can be defined for the plot options argument (plotptions) to control the appearance and dimensions of the image.
TIP: You can define n in specific GIF plot options. GIF plot options to use with the plotoptions argument are:
- height=n — Number of pixels, n, of the image height (default is 512).
- width=n — Number of pixels, n, of the image width (default is 512).
- colors=n — Number of colors, n (default is 256).
TIP: You can define n in specific JPEG plot options. JPEG plot options to use with the plotoptions argument are:
- height=n — Number of pixels, n, of the canvas image height (default is 360).
- width=n — Number of pixels, n, of the canvas width (default is 480).
- quality=n — JPEG quality level between 0 and 100, n (default is 95; there is negligible visible effect greater than 95).
Example —
plotmaple("plot(sin(x), x=-Pi..Pi), plotdevice='jpeg', plotoptions='height=250, width=250'");
- Returns:
plotmaple("plotstatement, libname, plotdevice, plotoptions") — runs the Maple code (plotstatement) after loading the custom Maple library located at the specified file path (libname). This function can also include the gif (to produce a GIF/ANIMATED-GIF) or jpeg (to produces a 24-bit color JPEG) inputs for the plot device argument (plotdevice). Display options can be defined for the plot options argument (plotptions) to control the appearance and dimensions of the image.
Example —
plotmaple("plotstatement, libname='filename.lib', plotdevice='gif|jpeg', plotoptions='options'");
- Returns a plot that references the name of the file in your Maple library alongside the plotstatement, plotdevice, and plotoptions arguments.
rand(m, n), rand(m, n, s)
rand(m,n) — Returns a random real number between m and n (inclusive).
Example —
rand(0.5, 9.5);
- Returns random numbers between 0.5 and 9.5.
rand(m,n,s) — Returns a random real number between m and n expressed to s (s>0) significant digits (s is truncated to an integer).
Example —
rand(2.73, 7.91, 2);
- Returns random numbers between 2.73 and 7.91 to 2 significant figures.
TIP: Combine the decimal function with the rand function to generate random numbers that vary in order of magnitude and have the same number of decimal digits.
Example —
decimal(1, rand(2, 20, 3));
- Returns random numbers between 2 and 20 with 1 decimal place.
NOTE: Numbers posing a possible ambiguity are returned using scientific notation.
Random integer generation: range(n), range(m, n), range(m, n, k)
The range function returns random integers from a range defined with a step size.
range(n) — n>=1 generates a random integer in the range 1, ..., floor(n) (inclusive). There are floor(n) numbers in that range. Therefore, it is a selection of 1 number from a choice of floor(n).
Example —
range(3);
- Returns 1, 2, or 3.
range(m,n) — n-m>=0 generates a random integer in the range m, m+1,..., m+q (inclusive), where q is the floor of n-m.
Example —
range(2,3);
- Returns 2 or 3.
range(m,n,k) — (n-m)/k=0 generates a random integer in the range m, m+k, ..., m+q*k (inclusive), where q is the floor of (n-m)/k.
Example —
range(0,7,3);
- Returns 0, 3, or 6.
Example —
range(0,8,3);
- Returns 0, 3, or 6.
Example —
range(0,9,3);
- Returns 0, 3, 6, or 9.
TIP: range(n) = range(1,n) = range(1,n,1)
NOTE: The rint function returns random numbers in the range 0, ..., n-1 (inclusive).
Random integer generation: rint(n), rint(m, n), rint(m, n, k)
The rint function returns random integers.
rint(n) — Generates a random integer in the range 0, ..., n-1 (inclusive). There are n numbers in that range. Therefore, it is a selection of one number from a choice of n.
Example —
rint(3);
- Returns 0,1, or 2.
rint(m,n) — Generates a random integer in the range m, ..., n-1 (inclusive).
Example —
rint(1,3);
- Returns 1 or 2.
rint(m,n,k) — Generates a random integer in the range m, m+k, ..., m+q*k (inclusive) where q is the largest integer such that m+q*k<=n-k.
Example —
rint(0,7,3);
- Returns 0 or 3.
Example —
rint(0,8,3);
- Returns 0 or 3.
Example —
rint(0,9,3);
- Returns 0,3, or 6.
TIP:rint(n) = rint(0,n) = rint(0,n,1)
NOTE: The range function returns random integers in the range 0, ..., n (inclusive).
rank(n, a, b, c, d, ...)
Returns the nth largest element item from a list ( numbering starts at 1).
Example —
rank(3, 2, 4, 6, 5, 7);
- Returns 5 (5 is the third largest number in the sequence)
Rounding: int(x), maple("MapleTA:-Builtin:-decimal(n, x)"), maple("MapleTA:-Builtin:-sig(n, x)")
int(x) — Returns the integer part of x.
Example —
int(20.8571);
- Returns 20
maple("MapleTA:-Builtin:-decimal(n, x)") — Returns x expressed as a floating-point number rounded to n decimal places through Maple. Trailing zeros are displayed.
Example —
maple("MapleTA:-Builtin:-decimal(3, 20.8577)");
- Returns 20.858
maple("MapleTA:-Builtin:-sig(n, x)") — Returns x expressed as a floating-point number rounded to n significant digits through Maple. In cases of possible ambiguity, scientific notation is used to display the value.
Example —
maple("MapleTA:-Builtin:-sig(3, 20.8571)");
Returns 20.9
Standard mathematical functions: sin(x), cos(x), tan(x), ...
Standard mathematical functions of x can also be used as algorithmic commands.
- sin(x), cos(x), tan(x)
- arcsin(x), arccos(x), arctan(x)
- csc(x), sec(x), cot(x)
- hypsin(x), hypcos(x), hyptan(x)
- archypsin(x), archypcos(x), archyptan(x)
- abs(x), sqrt(x)
- log(x), ln(x), exp(x)
Example —
tan(6);
- Returns -0.291006
Example —
sqrt(49);
- Returns 7
NOTE: This specific list of functions can be used by:
- Students when entering their responses to mathematical formula questions
- Authors and instructors when defining the correct response for a mathematical formula question
- Authors and instructors when authoring algorithmic questions
Statistical operations: binomial(n, r), maple("MapleTA[Builtin][erf](z)"), maple("MapleTA[Builtin][inverf](p)"), invstudentst(k, x), studentst(k, x)
binomial(n, r) — Computes the rth binomial coefficient of degree n. This corresponds to the number of ways of choosing r objects from a set of n, ignoring order.
Example —
binomial(22, 3);
- Returns the coefficient of x19 in (x+1)22 or 1,540.
maple("MapleTA[Builtin][erf](z)") — Computes the cumulative probability (probability that a variate assumes a value less than or equal to z) for a standard normal distribution (that is, with mean 0 and variance 1).
Example —
maple("MapleTA[Builtin][erf](0)");
- Returns 0.500000000000000
Example —
maple("MapleTA[Builtin][erf](1)");
- Returns 0.841344746068543
Example —
maple("MapleTA[Builtin][erf](2)");
- Returns 0.977249868051821
Example —
maple("MapleTA[Builtin][erf](3)");
- Returns 0.998650101968370
TIP: Other normal distributions can be modeled by re-normalizing (that is, erf((z-m)/s) is the probability distribution of a normal distribution with mean m and standard deviation s).
maple("MapleTA[Builtin][inverf](p)") — Computes the inverse of the cumulative probability for a standard normal distribution (that is, with mean 0 and variance 1). Let Z be a standard normally distributed random variable. Then maple("MapleTA[Builtin][inverf](p)") is the value of z for which P(Z<z) = p.
Example —
maple("MapleTA[Builtin][inverf](0.99)");
- Returns the value of z with probability 0.99 that Z<z.
invstudentst(k, x) — Computes the inverse of the cumulative probability density of the Students-t distribution with k degrees of freedom.
Example —
invstudentst(2, 0.9);
- Returns the value of x with probability equal to 0.9.
studentst(k, x) — Computes the cumulative probability distribution at x of the Students-t distribution with k degrees of freedom.
Example —
studentst(2, 1.55);
- Returns the probability that x<1.55.
strcat(a, b, c, d, ...)
Returns the concatenation of the strings in the list.
Example —
strcat("$a", " and ", "$b");
- Returns cats and dogs when $a="cats" and $b="dogs".
sum(varname, start, stop, expr)
Sums the expression (expr) with respect to the dummy variable (varname) between the values start and stop.
Example —
sum(i, 1, 20, i^2);
- Returns 2,870 (by evaluating 1^2 + 2^2 + 3^2 + ... + 20^2)
Example —
$s = sum(i, 1, $n, i^2);
- Returns the sum of the squares of the integers from 1 to n.
TIP: Don't use the $ character for the dummy variable in the summation.
switch(n, a, b, c, ...)
Given a whole number 0, 1, 2, ... and a list of items, the nth item in the list is returned based on position (the first item is in position 0, the second in position 1, and so on).
Example —
$prime=switch(rint(5), 2, 3, 5, 7, 11);
- Sets $prime to a random choice from the first 5 primes.
Example —
switch(1, "red", "green", "yellow");
- Returns green